
In this section we describe two more involved examples of using an IPython cluster to perform a parallel computation. In these examples, we will be using IPython’s “pylab” mode, which enables interactive plotting using the Matplotlib package. IPython can be started in this mode by typing:
ipython --pylab
at the system command line.
In this example we would like to study the distribution of digits in the number pi (in base 10). While it is not known if pi is a normal number (a number is normal in base 10 if 0-9 occur with equal likelihood) numerical investigations suggest that it is. We will begin with a serial calculation on 10,000 digits of pi and then perform a parallel calculation involving 150 million digits.
In both the serial and parallel calculation we will be using functions defined in the pidigits.py file, which is available in the docs/examples/parallel directory of the IPython source distribution. These functions provide basic facilities for working with the digits of pi and can be loaded into IPython by putting pidigits.py in your current working directory and then doing:
In [1]: run pidigits.py
For the serial calculation, we will use SymPy to calculate 10,000 digits of pi and then look at the frequencies of the digits 0-9. Out of 10,000 digits, we expect each digit to occur 1,000 times. While SymPy is capable of calculating many more digits of pi, our purpose here is to set the stage for the much larger parallel calculation.
In this example, we use two functions from pidigits.py: one_digit_freqs() (which calculates how many times each digit occurs) and plot_one_digit_freqs() (which uses Matplotlib to plot the result). Here is an interactive IPython session that uses these functions with SymPy:
In [7]: import sympy
In [8]: pi = sympy.pi.evalf(40)
In [9]: pi
Out[9]: 3.141592653589793238462643383279502884197
In [10]: pi = sympy.pi.evalf(10000)
In [11]: digits = (d for d in str(pi)[2:]) # create a sequence of digits
In [12]: run pidigits.py # load one_digit_freqs/plot_one_digit_freqs
In [13]: freqs = one_digit_freqs(digits)
In [14]: plot_one_digit_freqs(freqs)
Out[14]: [<matplotlib.lines.Line2D object at 0x18a55290>]
The resulting plot of the single digit counts shows that each digit occurs approximately 1,000 times, but that with only 10,000 digits the statistical fluctuations are still rather large:
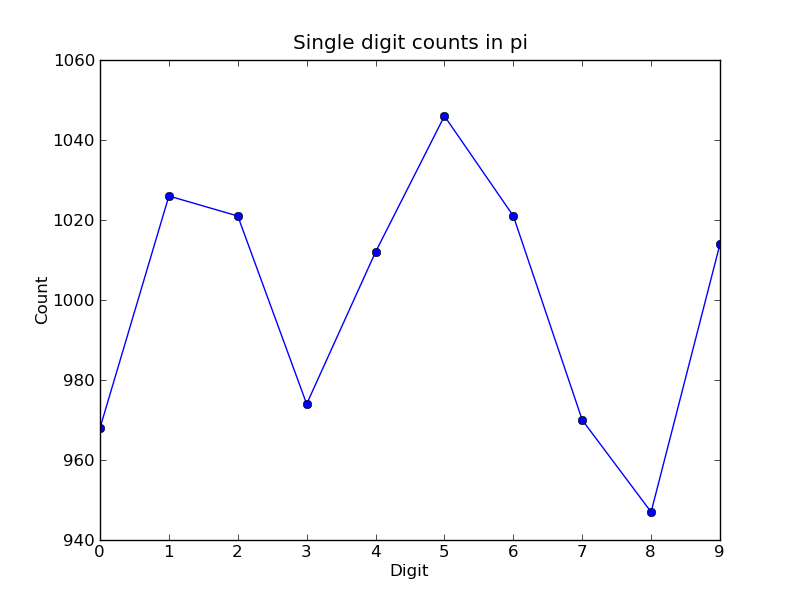
It is clear that to reduce the relative fluctuations in the counts, we need to look at many more digits of pi. That brings us to the parallel calculation.
Calculating many digits of pi is a challenging computational problem in itself. Because we want to focus on the distribution of digits in this example, we will use pre-computed digit of pi from the website of Professor Yasumasa Kanada at the University of Tokyo (http://www.super-computing.org). These digits come in a set of text files (ftp://pi.super-computing.org/.2/pi200m/) that each have 10 million digits of pi.
For the parallel calculation, we have copied these files to the local hard drives of the compute nodes. A total of 15 of these files will be used, for a total of 150 million digits of pi. To make things a little more interesting we will calculate the frequencies of all 2 digits sequences (00-99) and then plot the result using a 2D matrix in Matplotlib.
The overall idea of the calculation is simple: each IPython engine will compute the two digit counts for the digits in a single file. Then in a final step the counts from each engine will be added up. To perform this calculation, we will need two top-level functions from pidigits.py:
def compute_two_digit_freqs(filename):
"""
Read digits of pi from a file and compute the 2 digit frequencies.
"""
d = txt_file_to_digits(filename)
freqs = two_digit_freqs(d)
return freqs
def reduce_freqs(freqlist):
"""
Add up a list of freq counts to get the total counts.
"""
allfreqs = np.zeros_like(freqlist[0])
for f in freqlist:
allfreqs += f
return allfreqs
We will also use the plot_two_digit_freqs() function to plot the results. The code to run this calculation in parallel is contained in docs/examples/parallel/parallelpi.py. This code can be run in parallel using IPython by following these steps:
When run on our 16 cores, we observe a speedup of 14.2x. This is slightly less than linear scaling (16x) because the controller is also running on one of the cores.
To emphasize the interactive nature of IPython, we now show how the calculation can also be run by simply typing the commands from parallelpi.py interactively into IPython:
In [1]: from IPython.parallel import Client
# The Client allows us to use the engines interactively.
# We simply pass Client the name of the cluster profile we
# are using.
In [2]: c = Client(profile='mycluster')
In [3]: v = c[:]
In [3]: c.ids
Out[3]: [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14]
In [4]: run pidigits.py
In [5]: filestring = 'pi200m.ascii.%(i)02dof20'
# Create the list of files to process.
In [6]: files = [filestring % {'i':i} for i in range(1,16)]
In [7]: files
Out[7]:
['pi200m.ascii.01of20',
'pi200m.ascii.02of20',
'pi200m.ascii.03of20',
'pi200m.ascii.04of20',
'pi200m.ascii.05of20',
'pi200m.ascii.06of20',
'pi200m.ascii.07of20',
'pi200m.ascii.08of20',
'pi200m.ascii.09of20',
'pi200m.ascii.10of20',
'pi200m.ascii.11of20',
'pi200m.ascii.12of20',
'pi200m.ascii.13of20',
'pi200m.ascii.14of20',
'pi200m.ascii.15of20']
# download the data files if they don't already exist:
In [8]: v.map(fetch_pi_file, files)
# This is the parallel calculation using the Client.map method
# which applies compute_two_digit_freqs to each file in files in parallel.
In [9]: freqs_all = v.map(compute_two_digit_freqs, files)
# Add up the frequencies from each engine.
In [10]: freqs = reduce_freqs(freqs_all)
In [11]: plot_two_digit_freqs(freqs)
Out[11]: <matplotlib.image.AxesImage object at 0x18beb110>
In [12]: plt.title('2 digit counts of 150m digits of pi')
Out[12]: <matplotlib.text.Text object at 0x18d1f9b0>
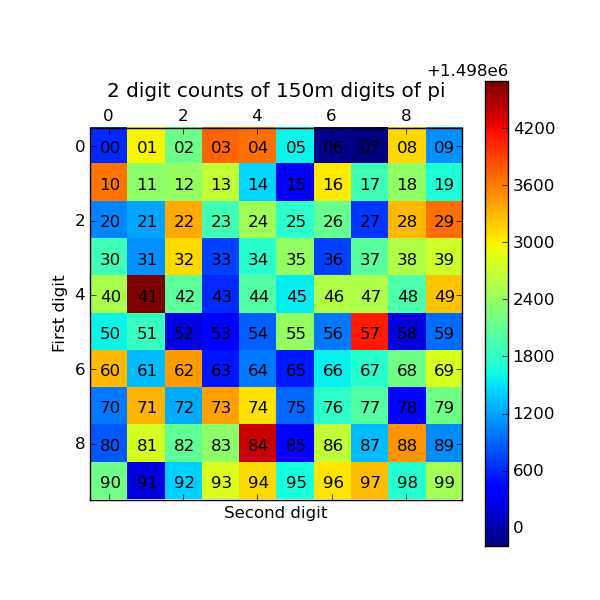
The resulting plot generated by Matplotlib is shown below. The colors indicate which two digit sequences are more (red) or less (blue) likely to occur in the first 150 million digits of pi. We clearly see that the sequence “41” is most likely and that “06” and “07” are least likely. Further analysis would show that the relative size of the statistical fluctuations have decreased compared to the 10,000 digit calculation.
An option is a financial contract that gives the buyer of the contract the right to buy (a “call”) or sell (a “put”) a secondary asset (a stock for example) at a particular date in the future (the expiration date) for a pre-agreed upon price (the strike price). For this right, the buyer pays the seller a premium (the option price). There are a wide variety of flavors of options (American, European, Asian, etc.) that are useful for different purposes: hedging against risk, speculation, etc.
Much of modern finance is driven by the need to price these contracts accurately based on what is known about the properties (such as volatility) of the underlying asset. One method of pricing options is to use a Monte Carlo simulation of the underlying asset price. In this example we use this approach to price both European and Asian (path dependent) options for various strike prices and volatilities.
The code for this example can be found in the docs/examples/parallel/options directory of the IPython source. The function price_options() in mckernel.py implements the basic Monte Carlo pricing algorithm using the NumPy package and is shown here:
def price_options(S=100.0, K=100.0, sigma=0.25, r=0.05, days=260, paths=10000):
"""
Price European and Asian options using a Monte Carlo method.
Parameters
----------
S : float
The initial price of the stock.
K : float
The strike price of the option.
sigma : float
The volatility of the stock.
r : float
The risk free interest rate.
days : int
The number of days until the option expires.
paths : int
The number of Monte Carlo paths used to price the option.
Returns
-------
A tuple of (E. call, E. put, A. call, A. put) option prices.
"""
import numpy as np
from math import exp,sqrt
h = 1.0/days
const1 = exp((r-0.5*sigma**2)*h)
const2 = sigma*sqrt(h)
stock_price = S*np.ones(paths, dtype='float64')
stock_price_sum = np.zeros(paths, dtype='float64')
for j in range(days):
growth_factor = const1*np.exp(const2*np.random.standard_normal(paths))
stock_price = stock_price*growth_factor
stock_price_sum = stock_price_sum + stock_price
stock_price_avg = stock_price_sum/days
zeros = np.zeros(paths, dtype='float64')
r_factor = exp(-r*h*days)
euro_put = r_factor*np.mean(np.maximum(zeros, K-stock_price))
asian_put = r_factor*np.mean(np.maximum(zeros, K-stock_price_avg))
euro_call = r_factor*np.mean(np.maximum(zeros, stock_price-K))
asian_call = r_factor*np.mean(np.maximum(zeros, stock_price_avg-K))
return (euro_call, euro_put, asian_call, asian_put)
To run this code in parallel, we will use IPython’s LoadBalancedView class, which distributes work to the engines using dynamic load balancing. This view is a wrapper of the Client class shown in the previous example. The parallel calculation using LoadBalancedView can be found in the file mcpricer.py. The code in this file creates a LoadBalancedView instance and then submits a set of tasks using LoadBalancedView.apply() that calculate the option prices for different volatilities and strike prices. The results are then plotted as a 2D contour plot using Matplotlib.
# <nbformat>2</nbformat>
# <markdowncell>
# # Parallel Monto-Carlo options pricing
# <markdowncell>
# ## Problem setup
# <codecell>
import sys
import time
from IPython.parallel import Client
import numpy as np
from mckernel import price_options
from matplotlib import pyplot as plt
# <codecell>
cluster_profile = "default"
price = 100.0 # Initial price
rate = 0.05 # Interest rate
days = 260 # Days to expiration
paths = 10000 # Number of MC paths
n_strikes = 6 # Number of strike values
min_strike = 90.0 # Min strike price
max_strike = 110.0 # Max strike price
n_sigmas = 5 # Number of volatility values
min_sigma = 0.1 # Min volatility
max_sigma = 0.4 # Max volatility
# <codecell>
strike_vals = np.linspace(min_strike, max_strike, n_strikes)
sigma_vals = np.linspace(min_sigma, max_sigma, n_sigmas)
# <markdowncell>
# ## Parallel computation across strike prices and volatilities
# <markdowncell>
# The Client is used to setup the calculation and works with all engines.
# <codecell>
c = Client(profile=cluster_profile)
# <markdowncell>
# A LoadBalancedView is an interface to the engines that provides dynamic load
# balancing at the expense of not knowing which engine will execute the code.
# <codecell>
view = c.load_balanced_view()
# <codecell>
print "Strike prices: ", strike_vals
print "Volatilities: ", sigma_vals
# <markdowncell>
# Submit tasks for each (strike, sigma) pair.
# <codecell>
t1 = time.time()
async_results = []
for strike in strike_vals:
for sigma in sigma_vals:
ar = view.apply_async(price_options, price, strike, sigma, rate, days, paths)
async_results.append(ar)
# <codecell>
print "Submitted tasks: ", len(async_results)
# <markdowncell>
# Block until all tasks are completed.
# <codecell>
c.wait(async_results)
t2 = time.time()
t = t2-t1
print "Parallel calculation completed, time = %s s" % t
# <markdowncell>
# ## Process and visualize results
# <markdowncell>
# Get the results using the `get` method:
# <codecell>
results = [ar.get() for ar in async_results]
# <markdowncell>
# Assemble the result into a structured NumPy array.
# <codecell>
prices = np.empty(n_strikes*n_sigmas,
dtype=[('ecall',float),('eput',float),('acall',float),('aput',float)]
)
for i, price in enumerate(results):
prices[i] = tuple(price)
prices.shape = (n_strikes, n_sigmas)
# <markdowncell>
# Plot the value of the European call in (volatility, strike) space.
# <codecell>
plt.figure()
plt.contourf(sigma_vals, strike_vals, prices['ecall'])
plt.axis('tight')
plt.colorbar()
plt.title('European Call')
plt.xlabel("Volatility")
plt.ylabel("Strike Price")
# <markdowncell>
# Plot the value of the Asian call in (volatility, strike) space.
# <codecell>
plt.figure()
plt.contourf(sigma_vals, strike_vals, prices['acall'])
plt.axis('tight')
plt.colorbar()
plt.title("Asian Call")
plt.xlabel("Volatility")
plt.ylabel("Strike Price")
# <markdowncell>
# Plot the value of the European put in (volatility, strike) space.
# <codecell>
plt.figure()
plt.contourf(sigma_vals, strike_vals, prices['eput'])
plt.axis('tight')
plt.colorbar()
plt.title("European Put")
plt.xlabel("Volatility")
plt.ylabel("Strike Price")
# <markdowncell>
# Plot the value of the Asian put in (volatility, strike) space.
# <codecell>
plt.figure()
plt.contourf(sigma_vals, strike_vals, prices['aput'])
plt.axis('tight')
plt.colorbar()
plt.title("Asian Put")
plt.xlabel("Volatility")
plt.ylabel("Strike Price")
# <codecell>
plt.show()
To use this code, start an IPython cluster using ipcluster, open IPython in the pylab mode with the file mckernel.py in your current working directory and then type:
In [7]: run mcpricer.py
Submitted tasks: 30
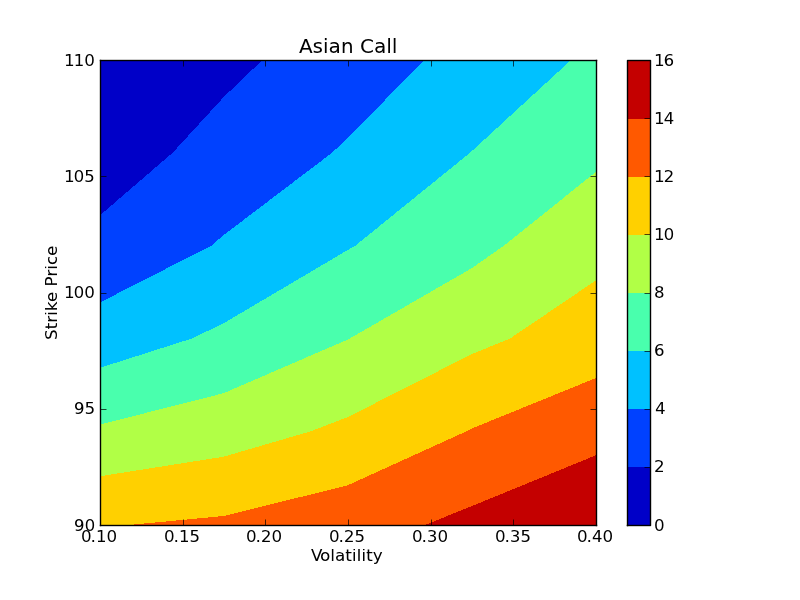
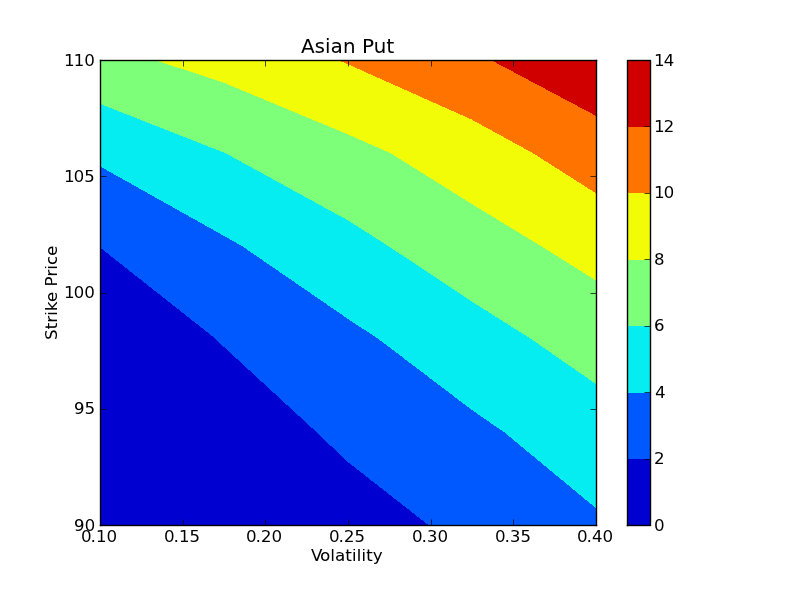
Once all the tasks have finished, the results can be plotted using the plot_options() function. Here we make contour plots of the Asian call and Asian put options as function of the volatility and strike price:
In [8]: plot_options(sigma_vals, strike_vals, prices['acall'])
In [9]: plt.figure()
Out[9]: <matplotlib.figure.Figure object at 0x18c178d0>
In [10]: plot_options(sigma_vals, strike_vals, prices['aput'])
These results are shown in the two figures below. On our 15 engines, the entire calculation (15 strike prices, 15 volatilities, 100,000 paths for each) took 37 seconds in parallel, giving a speedup of 14.1x, which is comparable to the speedup observed in our previous example.
To conclude these examples, we summarize the key features of IPython’s parallel architecture that have been demonstrated: